Let us begin by looking at how fusion can occur. This picture describes what the SM calls a square well potential, but actually the exact shape of the well doesn't matter at the moment. If we bring a charged particle in from the right, to one that is on the left, the curve predicts how much enegy we will need to overcome the Coloumb force to get it to touch, at the point labled a on the plot. If there were no such thing as quantum theory (not to mention reality) then we'd need to put in energy equal to or greater than that peak to get fusion to happen. IIRC (will have to look it up) for two particles with unit charge, and the radius of the deuteron, this would take around a mega electron volt to do. Luckily there is quantum reality, however. What it implies is that long before we get that close, it is possible for tunneling into the well to occur, or in simpler terms, for the particles to fuse. The closer they get, and the longer they are close, the higher the probability of fusion, to single out the case of an exogeric fusion reaction here. Perhaps one of my smarter and more pedantic friends can plug in Planck's constant and a little math and plot that, but for my purposes here, this is enough. This is a very good thing, or you'd have to have that megavolt to do fusion even in this easy case of two unit charge nuclei.
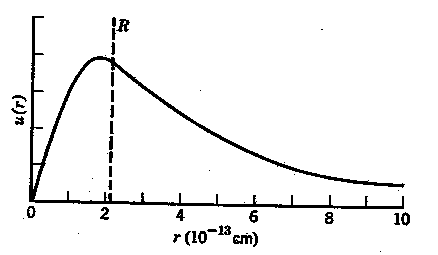To better picture this, here is a plot of the wave function of a deuteron. Notice it also has a "long tail", which in this case theoretically goes to infinite distance, but at very low probability at any distance far (on nuclear scales) from the center. In extemus, anytime the wave functions of two deuterons overlap, there can be fusion, with the likelyhood of that fusion having to do with how long, and how large the wavefunctions are where they overlap. As this function decays quite quickly with distance though, this is very unlikely unless you can get two close together for a fairly long time (on nuclear scales of space and time). This is why there are still fusible fuels in the universe, and it hasn't all gong bang on its own so far. As Rutherford proved, atoms are far larger than nuclei are, and by the time you've got say, a D2 molecule with electrons, the two nuclei are much father apart than is necessary for any reasonable, measurable, fusion rate to occur. For example, the bond length of an H2 atom is measured at about 74 picometres, or
about 7.4 e-9 cm. That's huge on the scale of this picture (4 orders magnitude) and at that distance the wavefunction probablilities of the two atoms overlap only a tiny amount. Which is why D2 doesn't just fuse on its own at STP, or so rarely we don't notice it ever doing it. Again, perhaps one of my smart friends can chime in and provide a plot of probablity vs time and space for this effect, but the upshot is, they have to be close, and stay close for a little while to fuse.
Once you have managed to get two of them close, it doesn't take physics "work" to keep them there, but in a practical sense, with what would you hold them? Nothing I know of, so the best you can do so far is to push them together head on. Given you're moving them at finite energy (required if you're going to have gain, after all) your best shot is to get them head on, close, and like a ball at the top of a trajectory (or a sine wave) they spend a lot of time before the repulsion moves them farther apart again. Glancing blows don't do nearly as well for this as head on (a good impact parameter) does. It is on this idea that the Lawson criterion is based, but in a beam on beam, non-thermal situation, the numbers come out differently than in a randomly moving set of particles in a plasma, which is what he covered. Assuming for the moment we can avoid thermalization and the spreading out of all our input energy into all the degrees of freedom, we have a better shot than Lawson would predict. But we are still reduced to firing deuterons (or other fusible fuels) at one another and hoping for hits, kind of like firing two shotguns at one another at a distance and hoping some of the shot hits -- only this shot repels other shot just to make it harder to do, so most of the shot and gunpowder are wasted. Obviously, one could consider gaming this situation by using shotguns with a lot more shot so they would throw up a continuous wall of lead, improving the odds, and essentially giving the repelled particles no way to escape. This would require, however, about 4 orders magnitude squared more than normal solid densities, and nothing on this planet has ever come even close to that. If you work out what the beam currents would be, even assuming you can have a one-atom wide beam, the numbers are pretty staggering, not even worth working out here, as humans are unlikely to get even close to them in well, forever, or the life of the sun to name a more finite number. You'd be on the verge of making black holes with that density, and if you can do that, no need for this!
Now, along comes this very smart kid named Philo T. Farnsworth, and he's got an idea, if not a perfect one. To very deeply paraphrase, he says, if we can't get a good hit rate, why not get another try with the same shotgun pellets, or in other words get the ions we've made (which costs some energy) to recirculate, and try again? This way, we can do this at manageable densities, and maybe get some energy gain out of the process. You get a lot of energy out of fusion, after all, about 3.4 MeV from DD, and it takes about 13.6 ev to strip an electron off a D atom, a little more (a couple eV) to take D2 apart, and about some tens of KeV to push them together close enough to get some probability of them fusing. After all, we're putting in some tens of KeV and maybe getting some Megavolts back out, so even a pretty small reaction rate gets us to net gain. A little off topic, but in a fusor, all the energy we put in also comes back out as heat along with any fusion energy, so the equation for net gain is slightly better than it otherwise would be, though we lose most of that in a practical situation where we get at best perhaps 40% of heat to electricity conversion in a normal power plant. Still, this is better than some other possibilities. But (heresy) Philo made one large mistake in his thinking. That's that a spring/mass class system would continue to oscillate in the presence of loss, which is what this picture shows -- everything visible here represents loss, or there'd be nothing to see at all. Fusion reaction products are not visible, neither the neutrons or the gamma rays can be seen. So there's just plain old loss, and any spring mass system will have oscillations die out without some stimulus that keeps putting energy in. There are mechanisms that exist that can take DC input and produce oscillation, but none of them are present in a standard fusor. So why do we see what we see? (and measure what we measure)
Note to self, draw pictures for this part and scan them.
I would like to propose that we measure what we do and see what we see is a dynamic equilibrium. This can look just like a steady state if you can't see atoms, and is what I thik is happening in a normal fusor run on DC input. There is no evidence of coherent particle motion. These are charged particles, and if a bunch of them move together, you get some radio waves that a 'scope will see, just like say in a klystron or a magnetron, a backward wave oscillator, or you name it, anything that takes in DC and puts out waves. We do NOT see evidence of that, and at the energies we are using, assuming the particles are going that input energy, we should see things in the 1-100 mhz region depending on harmonics, fusor size and actual particle speeds. In fact, if we see anything at all at any frequency we can measure (and past any that these particles can make acting in groups) it is noise.
So, what's really going on? No one really knows, but we are currently doing experiments to find out. Here is what I suspect, and which some of those experiments are beginning to bear out.
In a normal fusor, we have both ions (both flavors, monatomic and diatomic) and neutrals. The ratio is debatable at any set of operating conditions, but we always have at least all three of those, plus various contaminants. We apply a big DC field to this.
If we do this as a sharp step, all the ions begin to follow the field gradient towards the grid. But wait! They also produce their own field just by being ions. This means that any place they concentrate, the make their own fairly large field, and it does not take that many of them (reference some high school book here this is real basic), roughly the same ampere seconds we put into the grid vacuum capacity to charge it up in the first place, not many charges measured that way at all. But even ignoring that for the moment (but we can't forever) lets assume now that all the ions are flying to the grid and get the full applied field as their energy, and therefore speed. For now, pretend none hit the grid to be neutralized and waste input power. After getting the the grid center, possibly influenced by the lens-like field shape a grid with holes in it must make, they fly out again, this time expending their energy against the field gradient, and at some point, assuming any finite loss, they don't hit the outer wall and then return to the field that attracts them, and this repeats. There's your spring-mass class system, the basic harmonic oscillator. Oscillator is used here because the books overload that term to mean something very different from an RF or acoustic oscillator like probably sits on your bench, which takes DC input and makes Waves as output. Nope. This is just the resonant circuit, that we have put a step function on, and after that it follows all the normal rules (Fourier and others). Since there is loss -- you can see and measure it just fine, there is zero doubt about that, well, this dies down.
What then happens? We collect a lot of space charge in and around the grid, finally enough to cancel the large scale field from the grin in the tank. Due to thermalization and other effects, some ions hit the grid, pick up (and maybe knock out a few more) an electron, and are neutralized. Ions hitting these also tend to get thermalized, and the resulting energy transfer mediated by electron excitation makes the light we see. As ions hit the grid and are neutralized, the space charge no longer cancels the grid field, and more ions are pulled in. We wind up with this low density sea of relatively slow moving particles in and around the grid. More ions are created by electrons streaming off the grid due to impact secondaries to provide more, and the neutrals eventuall escape to make the neutral pressure gradient zero, the lowest energy state. Space charge neutralization by this mechanism never is perfect, leaving some fraction of the applied grid field-generating voltage available to draw in more ions at a decent, but less than applied voltage, speed. Some net gradient is needed to "keep the fusor lit" as any experimentalist will have observed. This is one very important explanation of why the normal fusor Q is so very low -- the particles aren't going as fast as you thought! Makes more sense when you look at the cross section plots at far lower energy, where the probability of tunneling through the Columb barrier is far less, because the particles can't get close enough classically to get to the place where quantum takes over very often -- it takes a lucky bump from another hot particle to get them the rest of the way there, but that is rare, as is say, the energy you can collect from Brownian motion, and for the same reasons. There are further problems with a static or dynamic equilibrium fusor that only make all this worse. Since most of what is going on energetically involves a big space charge around the grid, and beneficial lensing you might get with a good grid design is essentially degraded. I havn't worked out the numbers yet, but they are so poor that a realistic lens doesn't seem realistically a thing that can be made with the gradients involved, and at anything like the desired densities.
For reasons of Coulomb repulsion, you cannot get but a certain amount of particles to focus at once through say, a pipe or to a point in a beam -- any beam "blows up" as anyone who plays with this knows. The numbers get worse for luminosity at the longer focal lengths and lower fields and energies. This effect is way way more and results in focal densities far less than what quantum theory allows, this is classical physics all the way at this point. The way to increase luminosity is to increase the fields, the speeds of the particles (same thing depending on initial conditions) and shorten the focal length. The better those numbers become the more particles you can push through a voxel at a time. The more you can push through, the more will interact, the closer the situation becomes to shooting a shotgun at a wall, instead of another ones shot. Higher interaction rate, which we all crave for Q, as we have losses to overcome, they are always with us in any system of any complexity.
There is one more thing. Too much symmetry is bad. Yes, that's heresy, but here is why, at least assuming we want this to happen where and when we want, under our control, rather than depending on the gods of random chance (thermalization). With perfect and detailed symmetry, you have a large fraction of glancing blows of incoming beams. If the beams are at 90°, you still get .707 of that net collision energy, but it gets bad quick as you get to glancing angles, which more beams create more of. You can't cheat geometry and trigonometry. This is one reason why we are working in cylinders rather than spheres, but not the only one, as even our cylinders have too much symmetry at present, or so the math seems to indicate.
So, in looking to improve the performance of a Farnsworth fusor, we need a little heresy in his religion, but we haven't (and won't try to) prove we need it in the real universe either. There are "things we can do" here that don't need that and which do, experimentally, actually make substantive improvements in the Q of a fusor type setup.
Basically, we need to get the two charts at the top of this page happy together, so we need to push deuterons (or whatever) close enough for long enough to make that happen, and this seems to take luminosity, as we can't just clamp them in tweezers and push them together outside of imagination, or big bad weapons, which isn't what we want at all. We'd like to be able to hit a bullet with a bullet, head on, and get every ounce of accelerating energy into a good impact ratio collision on the first pass. If we can recirculate later the ones that miss, fine, but first we have to have a probability they ever hit at all, or at least that's one approach; if you don't have one, there's not a lot of point in the other. At any rate the experimentalist here seems to have found a way to do both. And he's reporting that we are running about 300 times the normal Q of a fusor in "static" mode doing it, and that this number is conservative. At the low repeat rate the experimenter is getting right now, and assuming no recirculation (yet), this works out to triple the neutron output at 1/100 the power input. our experimenter thinks it will be no big deal to both get a faster repetition rate, and recirculation to boot, but is more interested in the "Q per pass" right now, and there's only one of him, me.
Let's allow ourselves to imagine some kind of tough initial conditions. Maybe not that tough, but it won't happen by accident automagically either. Even if you're going to progress to cyclical at some point, you have to define a phase, a starting point. Let us assume we are looking at a cylindrical grid fusor end on, which is easy because I have a picture of that to show here.
Not the best for the discussion, this is a cylinder fusor end on the the more photogenic static mode, but it defines the physical geometry.For pedagogical purposes, let us imagine we've somehow managed to create a high density of ions in what would look like a pipe seen end on in this picture, at about the periphery of the outer walls, in this case, in our 6" pipe. We might do this by shoving ions into the system (See the bright thing on the left? It's doing that.) by some force, then once they get there, putting on a little repulsive field from the center, so they arrange themselves like that -- head towards the outer walls. We dare not do this much, or for long, else they will hit the now negatively charged walls, pick up electrons, and become neutral. But ions are cheap, and we can get an equilibria here up to a certain number of them -- they always repel one another and create their own field, so timing is involved if we want the non equilibrum case to obtain.
Once you got em where you want them, you place a very quick negative charge ramp waveform on the central grid. The idea is to collapse this thin wall pipe as a pipe shape. There are significant advanatges to this. All the repulsion is circumferential if the pipe wall is very thin, so we can collapse the pipe all at once without it "buckling" on us. At first, the grid just looks like a point attractor, the wire spacing and so forth doesn't matter. As we crush the pipe, it gets harder and harder to do, as we are storing energy in the motion of particles closer to each other as they converge on center. This is why we ramp the voltage, to keep the net field more or less either constant or increasing with time, and as we bunch the ions closer together then field near them increases with their density and it becomes harder to continue accelerating them. At some point, they begin to traverse our grid, which to them looks like a bunch of long cylindrical optical lenses would, all focused at the central point if we do our part. The trick here is to turn this bunched-in-time incoming pipe walls, into rays that focus into the middle region, as fine as we can focus them, which is fine indeed if quantum theory limits are all there are (no, we can't do it that well, but real good is enough). To do this, we have to continue our ramp so as to cancel the ion space charge as it flows through the grid wires and distorts the normal field by doing so. Then, blam, we hope, they all hit in the middle, the more we can get in there in a small space-time, the greater the interaction ratio, it goes up as a square function, and even at ion speeds, they stay close for a long time compared to quantum tunneling times.
We continue the negative ramp as they pass through, to slow them down and get them ready for the next cycle, hopefully stopping them and turng them around before they reach the walls. Once we have them near but off the walls and coming back, repeat the entire process; go back to ground or even positive on the grid to bunch them again and repeat. Boom, high repetition rate which is equal to recirculation rate, if again we do our part with the correct arbitrary drive waveform. All we need is about the same level of sophistication as is used in a mass spectrometer, here with different intent and enough space charge to make the calculations more difficult. It won't be a sine wave!
This idea isn't new, it is what is called Barkenhausen oscillation in triode electron tubes, but here we are driving them to actually hit, and with significant energy. Because the whole time they are incoming they only see sideways forces, there is no pre existing space charge at grid center to repel them, and by the time they pass our lens, they are going fast enough that this only slows them down a little, but doesn't spoil focus, there is just not the time to make them deflect, and they won't tend to in the uniform field inside the grid -- which is uniform with or without the other ions coming in from all directions, again if we've done our part.
Nor are we limited to making an inside out triode here, we can use more grids, but not in the way many others concieve. We could have an outer, control grid that sits at a small negative potential to gather ions in and around it, and any losses due to ions hitting it would be at low energy, just like in a vacuum tetrode. Our inner grid is then a screen grid, and this "tube" is a screen driven electrometer tube, inside out. In other words, there is ample precedent for this one, nothing new here at all. All developed well before most of us were born at all, just thought about a little differently for a different application. So, no actual heresy is needed here, just the appearance to those who don't understand it all yet.